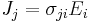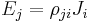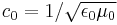Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities (especially kinetic quantities are related to kinematic quantities) that is specific to a material or substance, and approximates the response of that material to external forces. It is combined with other equations governing physical laws to solve physical problems, like the flow of a fluid in a pipe, or the response of a crystal to an electric field.
As an example, in structural analysis, constitutive relations connect applied stresses or forces to strains or deformations. The stress-strain constitutive relation for linear materials is commonly known as Hooke's law.
Some constitutive equations are simply phenomenological; others are derived from first principles. A common approximate constitutive equation frequently is expressed as a simple proportionality using a parameter taken to be a property of the material, such as electrical conductivity or a spring constant. However, much more elaborate constitutive equations often are necessary to account for tensor properties, the rate of response of materials and their non-linear behavior.[1] See the article Linear response function.
The first constitutive equation (constitutive law) was developed by Robert Hooke and is known as Hooke's law. It deals with the case of linear elastic materials. Following this discovery, this type of equation, often called a "stress-strain relation" in this example, but also called a "constitutive assumption" or an "equation of state" was commonly used. Walter Noll advanced the use of constitutive equations, clarifying their classification and the role of invariance requirements, constraints, and definitions of terms like "material", "isotropic", "aeolotropic", etc. The class of "constitutive relations" of the form stress rate = f (velocity gradient, stress, density) was the subject of Walter Noll's dissertation in 1954 under Clifford Truesdell.[2]
In modern condensed matter physics, the constitutive equation plays a major role. See Linear constitutive equations and Nonlinear correlation functions.[3]
Following are numerous examples of constitutive equations, many in frequent use.
Contents |
Matter
Definitions
| Nomenclature |
|---|
| F = friction force (N) R = reaction force at point of contact (N) |
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Static, kinetic, and rolling friction coefficients | μ, μf | 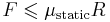
Normal force to a surface: |
dimensionless | dimensionless |
Definitive laws
| Property/effect | Equation |
|---|---|
| Hooke's law, defines elasticity/spring constants | Scalar forms: 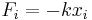 or Tensor forms, |
| F = tensile/compressive force (N) x = extended/contracted displacement (m) |
|
| Newton's law of experimental impact, defines coefficient of restitution | 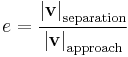
Usually |
| e = Coefficient of restitution vseparation = relative velocity of separation (m s−1) |
Transport phenomena
| Nomenclature |
|---|
| x = displacement of substance(m) A = Cross-section Area(m2) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Drag equation, drag coefficient | cd | 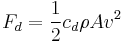 |
dimensionless | dimensionless |
Definitive laws
| Property/effect | Equation |
|---|---|
| Fick's law of diffusion, defines diffusion coefficient D | 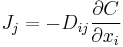 |
| D = mass diffusion coefficient (m2 s−1) J = diffusion flux of substance (mol m−2 s−1) |
|
| Darcy's law for porous flow in matter, defines permeability κ | 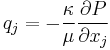 |
| κ = permeability of medium (m2) q = discharge flux of substance (m s−1) |
Equations
| Property/effect | Equation |
|---|---|
| Terminal velocity | 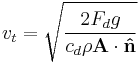 |
| vt = terminal velocity within fluid (m s-1) |
|
| Newtonian fluid | 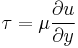 |
| τ = shear stress exerted by fluid (Pa) ∂u/∂y = velocity gradient perp. to shear direction, strain rate (s−1) |
Thermodynamics
| Nomenclature |
|---|
| L = length of material (m) Δx = Displacement of heat transfer (m) T = Temperature (K) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| General heat capacity | C = Heat capacity | 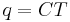 |
J K−1 | |
| Linear thermal expansion | α = Linear coefficient of linear thermal expansion | 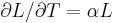
|
K−1 | [Θ]−1 |
| Volumetric thermal expansion | β, γ | 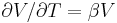 |
K−1 | |
| Thermal conductivity | κ, K, λ | 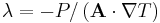 |
W m−1 K−1 | |
| Thermal conductance | U | 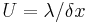 |
W m−2 K−1 | |
| Thermal resistance | R | 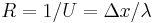 |
m2 K W−1 |
Definitive laws
| Property/effect | Equation |
|---|---|
| Fourier's law of thermal conduction, defines thermal conductivity λ | 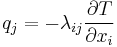 |
| λ = Thermal conductivity (W m−1 K−1 )
q = heat flux (W m−2) |
|
| Stefan–Boltzmann law of black-body radiation, defines emmisivity ε | For a single radiator:
For a temperature differance:
|
| I = radiant intensity (W m−2) σ = Stefan–Boltzmann constant (W m−2 K−4) |
|
| Ideal gas law, defines parameters of an ideal gas | 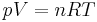 |
| p = pressure (Pa) T = temperature (K) |
Electromagnetism
In both classical and quantum physics, the precise dynamics of a system form a set of coupled differential equations, which are almost always too complicated to be solved exactly, even at the level of statistical mechanics. In the context of electromagnetism, this remark applies to not only the dynamics of free charges and currents (which enter Maxwell's equations directly), but also the dynamics of bound charges and currents (which enter Maxwell's equations through the constitutive relations). As a result, various approximation schemes are typically used.
For example, in real materials, complex transport equations must be solved to determine the time and spatial response of charges, for example, the Boltzmann equation or the Fokker–Planck equation or the Navier-Stokes equations. For example, see magnetohydrodynamics, fluid dynamics, electrohydrodynamics, superconductivity, plasma modeling. An entire physical apparatus for dealing with these matters has developed. See for example, linear response theory, Green–Kubo relations and Green's function (many-body theory).
These complex theories provide detailed formulas for the constitutive relations describing the electrical response of various materials, such as permittivities, permeabilities, conductivities and so forth.
| Nomenclature |
|---|
| E = electric field (N C−1) D = electric displacement field (Cm−2) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Electrical resistance | R | 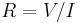 |
Ω = V A−1 = J s C−2 | [M] [L]2 [T]−3 [I]−2 |
| Resistivity | ρ | 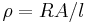 |
Ω m | [M]2 [L]2 [T]−3 [I]−2 |
| Resistivity temperature coefficient, linear temperature dependence | α | 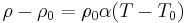 |
K−1 | [Θ]−1 |
| Electrical conductance | G | 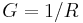 |
S = Ω−1 | [T]3 [I]2 [M]−1 [L]−2 |
| Electrical conductivity | σ | 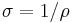 |
Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 |
| Relative permittivity (aka dielectric constant) | εr | can only be found from experiment | F m−1 | [I]2 [T]4 [M]−1 [L]−3 |
| (Absolute) dielectric permittivity | ε | 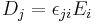 |
F m−1 | [I]2 [T]4 [M]−1 [L]−3 |
| Electric susceptibility | χE | 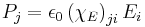 |
dimensionless | dimensionless |
| Magnetic reluctance | R, Rm, 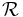 |
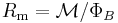 |
A Wb-1 = H-1 | [M]-1[L]-2[T]2 |
| Magnetic permeance | P, Pm, Λ, 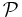 |
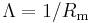 |
Wb A-1 = H | [M][L]2[T]-2 |
| Relative permeability | μr | can only be found from experiment | dimensionless | dimensionless |
| Absolute magnetic permeability | μ | 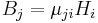 |
H m−1 | |
| Magnetic susceptibility | χM | 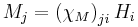 |
dimensionless | dimensionless |
Relations
| Property/effect | Equation |
|---|---|
| Electric field vectors | 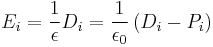 |
| Magnetic field Vectors | 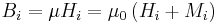 |
| Permittivity |  |
| Permeability | 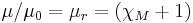 |
Laws
| Property/effect | Equation |
|---|---|
| Ohm's law of electric conduction, defines electric conductivity (and so resistivity and resistance) |
Simplist form is: 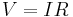
More general forms are: |
| J = Electric Current Density (A m−2) σ = Electric Conductivity (Ω−1 m−1) |
Photonics
| Nomenclature |
|---|
| c = luminal speed in medium (m s−1) c0 = luminal speed in vacuum (m s−1) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Refractive index | n | 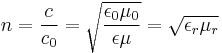 |
dimensionless | dimensionless |
Relations
| Property/effect | Equation |
|---|---|
| Luminal speed in matter | 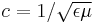 for special case of vacuum; ε = ε0 and μ = μ0, |
Solid state physics
These constitutive equations are often used in crystallography - a field of solid state physics.[4]
| Nomenclature |
|---|
| x = displacement (m) s = thickness of hall/probe (m) σ = mechanical stress (Pa) e = electron charge (C) T = temperature (K) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Pyroelectricity, pyroelectric coefficient | p | 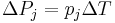 |
C m−2 K−1 | |
| Electrocaloric effect, pyroelectric coefficient | p | 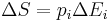 |
C m−2 K−1 | [I][T][L]-2[Θ]-1 |
| Seebeck effect, thermopower coefficient | β | 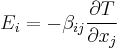 |
V K−1 | |
| Hall effect, Hall coefficient | RH | 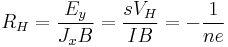 |
C-1 | [I]-1[T]-1 |
| Peltier effect, peltier coefficient | Π | 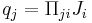 |
W A−1 | |
| Direct piezoelectric effect, direct piezoelectric coefficient | d, de | 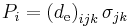 |
K−1 | |
| Converse piezoelectric effect, direct piezoelectric coefficient | d, de' | 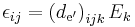 |
K−1 | |
| Piezomagnetic effect, piezomagnetic coefficient | q, dm | 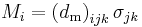 |
K−1 | |
| Piezooptic effect, piezooptic coefficient | Π | 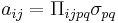 |
K−1 |
Equations
| Property/effect | Equation |
|---|---|
| Hall effect | 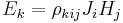 |
See also
References
- ^ Clifford Truesdell & Walter Noll; Stuart S. Antman, editor (2004). The Non-linear Field Theories of Mechanics. Springer. p. 4. ISBN 3540027793. http://books.google.com/books?id=dp84F_odrBQC&pg=PR13&dq=%22Preface+%22+inauthor:Antman.
- ^ See Truesdell's account in Truesdell The naturalization and apotheosis of Walter Noll. See also Noll's account and the classic treatise by both authors: Clifford Truesdell & Walter Noll - Stuart S. Antman (editor) (2004). "Preface" (Originally published as Volume III/3 of the famous Encyclopedia of Physics in 1965). The Non-linear Field Theories of Mechanics (3rd ed.). Springer. p. xiii. ISBN 3540027793. http://books.google.com/books?id=dp84F_odrBQC&pg=PR13&dq=%22Preface+to+the+Third%22+inauthor:Antman.
- ^ Jørgen Rammer (2007). Quantum Field Theory of Nonequilibrium States. Cambridge University Press. ISBN 9780521874991. http://books.google.com/books?id=A7TbrAm5Wq0C&pg=PR1&dq=isbn:9780521874991#PPA151,M1.
- ^ http://www.mx.iucr.org/iucr-top/comm/cteach/pamphlets/18/node2.html
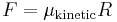
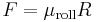
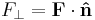
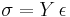
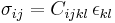
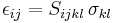
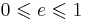 ,
,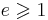
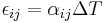
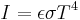
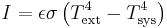
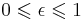
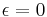 for perfect reflector
for perfect reflector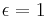 for perfect absorber (true black body)
for perfect absorber (true black body)